Proyección ortogonal de un punto sobre una recta
La sombra producida por una figura depende de la posición del foco luminoso que incide sobre ella.Por ejemplo, la sombra que forma un árbol al mediodía es una proyección ortogonal del árbol sobre el suelo, porque los rayos del Sol inciden perpendicularmente.
Sea A un punto y sea l una recta cualquiera, se llama proyección ortogonal de A sobre l al punto de intersección A entre la recta l y la recta perpendicular a l que pasa por A. Esa recta perpendicular se llama la proyectante de A sobre l.
Gráficamente esto es:

Proyección ortogonal de una línea sobre una recta
En la siguiente figura, el segmento AB es la proyección ortogonal de la línea l sobre la recta.
Para determinar la proyección ortogonal de una línea cualquiera sobre una recta, se deben buscar las proyecciones ortogonales de su origen y su extremo; el segmento determinado por dichas proyecciones será la proyección de dicha línea original.

La proyección ortogonal de una línea l sobre una recta es la unión de todas las proyecciones ortogonales de cada uno de los puntos de l sobre la recta.
- Proyección de un punto sobre una recta:
Dados los puntos P y dos rectas, m y n perpendiculares en X, de modo que el punto P no está en ninguna de ellas, explicar por qué al hallar las proyecciones ortogonales P´y P´´, la figura P´´XP´P que su formma es un rectangulo.
Procedimiento:
Se analiza el gráfico y se justifican los procedimientos usando las definiciones de proyección ortogonal, de rectas perpendiculares y la propiedad de los cuadriláteros:
Los ángulos en P´ y P´´ son rectos ya que son proyecciones ortogonales de P. El ángulo en X también es recto porque m y n son perpendiculares.
Como los cuadriláteros tienen la propiedad de que la suma de sus ángulos interiores es 360°, se deduce que el ángulo en P también mide 90°, por lo que todos los ángulos interiores de P´´ XP´´ P son rectos. En consecuencia, la figura es un rectángulo.
-Proyección de un segmento sobre una recta: proyectar un segmento sobre una recta dependerá de la posición del segmento con respecto a la recta.
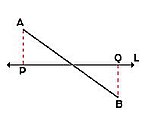
1) Si el segmento dado AB no es paralelo la recta L, la proyección ortogonal es segmento PQ que se obtiene trazando líneas perpendiculares a L desde los puntos extremos. La magnitud de la proyección siempre es menor que la del segmento dado.
Dados los puntos P y dos rectas, m y n perpendiculares en X, de modo que el punto P no está en ninguna de ellas, explicar por qué al hallar las proyecciones ortogonales P´y P´´, la figura P´´XP´P que su formma es un rectangulo.
Procedimiento:
Se analiza el gráfico y se justifican los procedimientos usando las definiciones de proyección ortogonal, de rectas perpendiculares y la propiedad de los cuadriláteros:
Los ángulos en P´ y P´´ son rectos ya que son proyecciones ortogonales de P. El ángulo en X también es recto porque m y n son perpendiculares.
Como los cuadriláteros tienen la propiedad de que la suma de sus ángulos interiores es 360°, se deduce que el ángulo en P también mide 90°, por lo que todos los ángulos interiores de P´´ XP´´ P son rectos. En consecuencia, la figura es un rectángulo.
-Proyección de un segmento sobre una recta: proyectar un segmento sobre una recta dependerá de la posición del segmento con respecto a la recta.
1) Si el segmento dado AB no es paralelo la recta L, la proyección ortogonal es segmento PQ que se obtiene trazando líneas perpendiculares a L desde los puntos extremos. La magnitud de la proyección siempre es menor que la del segmento dado.
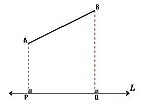
2) Si el segmento PQ y la recta L son paralelos, la proyección será: AB = PQ, que se obtiene de forma análoga.
3) Si el segmento AB tiene un punto común con la recta L, la proyección se obtiene de modo similar.

4) Si el segmento AB corta a la recta L, la proyección se obtiene de forma análoga.

Ejemplo : Trazar la proyección de AB sobre m y n.
Procedimiento:
Se trazan por A y B rectas perpendiculares a m para determinar el segmento PQ.
Se trazan por A y B rectas perpendiculares a n para hallar el segmento XY, y obtener la otra proyección buscada.
-Proyección de una figura sobre una recta: La proyección de las figuras planas, es decir, que tienen dos dimensiones: largo, ancho, origina proyecciones en una sola dimensión. Las proyecciones ortogonales de cuerpos, es decir, que tiene tres dimensiones: largo, ancho y alto, son figuras planas; tal como pasa con la sombra de un cuerpo cuando es iluminado por el Sol.

No hay comentarios:
Publicar un comentario