Simetría Axial

Simetría 

Muchos seres vivos, como por ejemplo las mariposas, tienen simetría en su cuerpo. A continuación se observa el dibujo de una mariposa y de una recta s, en el cual se puede ver la simetría de sus alas pues, cuando la mariposa las junta, estas coinciden.

Existen distintos tipos de simetría, entre ellas la simetría axial.

Simetría Axial

Es una transformación del plano o del espacio en la cual, a cada punto P, se asocia otro punto P' llamado imagen de P, de manera que P y P' están a igual distancia de una recta llamada eje de simetría, y el segmento PP' es perpendicular a dicho eje.

En la imagen anterior se observa el triángulo A'B'C' que es la imagen simétrica del triángulo ABC respecto aleje de simetría e. Se puede comprobar que:

- El eje de simetría es mediatriz de cualquier segmento que surja de unir un vértice con su imagen, por ejemplo AA'.

-Dos segmentos que sean uno imagen simétrica del otro tienen igual medida, por ejemplo AB= A'B'.

-Los ángulos que sean uno imagen simétrica del otro como el ángulo de B y B' tienen igual medida. 

Imagen simétrica de un segmento

La imagen simétrica de un segmento, dado un eje de simetría, se determina hallando la imagen de cada extremo del segmento, luego se traza el segmento que une ambas imágenes.

Ejemplo:

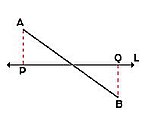
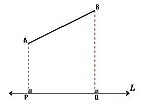
Determinar la imagen simétrica del segmento AB respecto a la recta m.

Procedimiento:

1.  Se trazan rectas perpendiculares a m por A y B. Se marca el punto A' tal que su distancia al eje m sea igual que del eje m a A. De igual forma para B'.
2.  Se unen las imágenes A' y B', y el segmento A'B', respecto al eje de simetría m.

Imagen simétrica de un polígono y de una circunferencia respecto a un eje de simetría

La imagen simétrica de un polígono respecto a un eje de una simetría se parece mucho a la imagen de un objeto reflejado en un espejo. Para determinarla se halla la imagen simétrica de cada uno de los vértices del polígono, de la misma forma como se determinó la imagen simétrica de un segmento, luego se unen.

Ejemplo:

Determinar la imagen simétrica del trapecio ABCD respecto a l.

Procedimiento:

1. Se determinan las imágenes simétricas A', B', C' y D' de los puntos A,B,C y D  respectivamente.
2. Se unen los puntos obtenidos para formar el polígono.

Para trazar el eje de la imagen simétrica de una circunferencia se halla la imagen simétrica de su centro respecto al eje y, luego, con el mismo radio, se dibuja la nueva circunferencia. A la derecha se muestra la imagen simétrica de la circunferencia de centro O y radio k, con respecto a m.

Rotaciones

Los movimientos rotatorios

Algunos elementos de la naturaleza o algunos objetos, describen movimientos de rotación, bien sea en sí mismos o con respecto a otro. Por ejemplo, la Luna con respecto a la Tierra genera un movimiento de rotación pues gira alrededor de ella, pero también la Tierra en sí realiza el mismo movimiento.

Ángulos dirigidos 

Cuando se describe un movimiento de rotación se genera un ángulo. 

El ángulo dirigido tiene un lado inicial y un lado final. Se dice que el ángulo dirigido es positivo si el giro que transforma un lado del ángulo en el otro es en sentido contrario a las agujas del reloj, mientras que es negativo si el sentido es igual al de las agujas del reloj.

A la medida de un ángulo, sin importar el sentido del mismo, se le llama amplitud del ángulo.

Rotación en el plano 

Si se tiene un punto O fijo en el plano y un angulo dirigido, la rotación de centro O y ángulo de un punto P cualquiera es una transformación en el plano que asigna a P un punto único P' llamado imagen de P, tal que  OP  = OP´, y la med(POP´) = α. Esta rotación se puede denotar por Rα (P) = P´.

Simetría central

Para hallar la imagen de cualquier punto P del plano bajo un ángulo de rotación es preciso conocer el ángulo dirigido y el centro de la rotación.

La simetría central de un punto o figura es una rotación de 180°. 

Rotación de segmentos

La imagen de un segmento, bajo cualquier rotación, se determina hallando los puntos que son imagen de los extremos que forman un segmento, y luego trazando el segmento que une ambos puntos.

Un segmento y su imagen bajo una rotación tienen igual longitud.

Rotación de un polígono
La imagen de un polígono bajo cualquier rotación, se determina hallando la imagen de cada uno de sus vértices bajo la rotación. Y luego uniendo los vértices hallados. 

Por ejemplo los cubos de Rubik tienen un centro de rotación que permite girar las caras del cubo en cualquier dirección.  

                                                        
Rotación de un  polígono en el plano cartesiano
Para hallar la imagen de un polígono en el plano cartesiano bajo una rotación, se determina la imagen de cada vértice y se hallan las coordenadas de los vértices de la imagen del polígono original.

Determinación del centro de rotación 
Conocer el centro de rotación de un objeto, resulta conveniente para calcular el movimiento que realizará el mismo. Por ejemplo, para que la rueda de un carro funcione a la perfección, el eje de la rueda debe ubicarse justo en el centro de rotación, de lo contrario, la rueda perdería estabilidad.
De igual manera, si se quiere determinar el centro de rotación de un segmento o polígono, se trazan segmentos que  unan dos extremos o vértices y con las mediatrices de esos segmentos se encuentra el centro de rotación.
Ejemplo:
Sea el triángulo X'Y'Z' la imagen del triángulo XYZ bajo la rotación de centro y ángulo de amplitud y sentido desconocidos . ¿ Cuál es el centro y el ángulo de la rotación?
Procedimiento:

1. Se trazan líneas que unan dos vértices con sus respectivas imágenes. En este caso se unió Y con Y' y Z con Z'.

2. Se dibujan las mediatrices de los segmentos trazados, se prolongan hasta quese corten entre sí y se marca el punto de intersección el cual es el centro de rotación.

3. Se une uno de los vértices y el de su imagen con el centro de rotación. En este caso, se unieron y, y' con el centro 0.

4. Se determina la amplitud y el sentido del ángulo. Para ello, se mide con un transportador el ángulo y se observa hacia qué posición está el polígono inicial y hacia qué lado quedó la imagen.

Traslaciones

Transformaciones en el plano

Cuando una persona se desplaza desde una posición a , se dice que hizo una transformación en el espacio. Si se traslada un punto o una figura, se experimenta una transformación en el plano. Una transformación en el plano es una correspondencia biunívoca sobre el plano, es decir, es una función f  que asigna a cada punto P del plano otro punto P´, único, llamado imagen de P.

Esta función es inyectiva, es decir, que cumple con que dos puntos distintos tienen imágenes distintas.

Algunas de las transformaciones en el plano son: traslación, rotación y simetría, las cuales representan movimientos en el plano que conservan la forma y el tamaño de la figura.

Traslación

Se puede hallar la imagen de un punto cualquiera a través de una traslación según un vector dado. Para ello se traza un vector equipolente al dado, cuyo origen sea el punto.

Ejemplo :

Determinar la imagen del punto P a través de una traslación por el vector u.

Procedimiento 

Se traza un vector equipolente a u cuyo origen sea el punto P.

Se marca el punto P´que es la imagen de P.

En general, la imagen de un punto P, bajo una traslación con un vector u, es una transformación en el plano que asigna a cada punto P un único punto P´ tal que los vectores PP y u sean equipolentes. El vector u se denomina vector de traslación.

La traslación según el vector u se denota mediante Tu . Por ejemplo, la expresión Tu (P) = P´ se denota que P´es la imagen del punto P bajo la traslación Tu.

Traslaciones en el plano cartesiano 

Para hallar la imagen de un punto M dado un vector de traslación u , se traza un vector equipolente al vector u partiendo de M. El punto extremo del vector trazado es la imagen de M según Tu, es decir, es M´. 

Cálculo de las coordenadas de la imagen de un punto 

Para obtener las coordenadas de un punto, que es imagen de otro dado mediante un vector de traslación, se usa la propiedad que indica que los componentes de dos vectores equipolentes son iguales.

Traslación de un segmento

La imagen de  un segmento, mediante un vector de traslación, se determina hallando las imágenes de los extremos del segmento a través del mismo vector y trazando el segmento que une las imágenes. 

   

Traslación de un ángulo

La imagen de un ángulo por una traslación, es un ángulo de igual medida al ángulo dado con sus lados respectivos paralelos entre sí. Para determinarla se hallan las imágenes del vértice y luego las imágenes de las semirrectas que conforman el ángulo.

Traslación de un polígono 

La imagen de un polígono bajo cualquier traslación se determina hallando la imagen de cada uno de los lados que forman el polígono. Para ello, se halla la imagen de los vértices que lo forman y luego se trazan los lados respectivos. 

Traslación de una circunferencia

Para hallar la imagen de una circunferencia de centro O y radio k mediante un vector de traslación u, se halla la imagen de centro O, a saber O´, y la imagen de un punto cualquiera de la circunferencia, llámese A dicho punto A´su imagen. La imagen de la circunferencia inicial es la circunferencia de centro O´y del mismo radio que k.

Composición de traslaciones  

Si a un punto se le aplica una traslación con vector u y a su imagen se le aplica una traslación de vector v, el punto obtenido es la imagen del punto inicial a través de una composición de traslaciones. Es decir, si P´ es la imagen del punto P bajo la traslación Tu y P´´ es la imagen de P´ bajo la traslación Tv, entonces P´´= Tu ( P´). La composición de ambas traslaciones, se denota por Tv[Tu (P)].

Proyecciones Ortogonales

Proyección ortogonal de un punto sobre una recta

La sombra producida por una figura depende de la posición del foco luminoso que incide sobre ella.Por ejemplo, la sombra que forma un árbol al mediodía es una proyección ortogonal del árbol sobre el suelo, porque los rayos del Sol inciden perpendicularmente.

Sea A un punto y sea l una recta cualquiera, se llama proyección ortogonal de A sobre l al punto de intersección A entre la recta l  y la recta perpendicular a l que pasa por A. Esa recta perpendicular se llama la proyectante de A sobre l.

Gráficamente esto es: 

                                        

Proyección ortogonal de una línea sobre una recta

En la siguiente figura, el segmento AB es la proyección ortogonal de la línea l sobre la recta. 

Para determinar la proyección ortogonal de una línea cualquiera sobre una recta, se deben buscar las proyecciones ortogonales de su origen y su extremo; el segmento determinado por dichas proyecciones será la proyección de dicha línea original.

                                              

La proyección ortogonal de una línea l sobre una recta es la unión de todas las proyecciones ortogonales de cada uno de los puntos de l sobre la recta.

Casos particulares de la proyección ortogonal 

- Proyección de un punto sobre una recta: 
Dados los puntos P y dos rectas, m y n perpendiculares en X, de modo que el punto P no está en ninguna de ellas, explicar por qué al hallar las proyecciones ortogonales P´y P´´, la figura P´´XP´P que su formma es un rectangulo. 

Procedimiento:
Se analiza el gráfico y se justifican los procedimientos usando las definiciones de proyección ortogonal, de rectas perpendiculares y la propiedad de los cuadriláteros:
Los ángulos en P´ y P´´ son rectos ya que son proyecciones ortogonales de P. El ángulo en X también es recto porque m y n son perpendiculares.
Como los cuadriláteros tienen la propiedad de que la suma de sus ángulos interiores es 360°, se deduce que el ángulo en P también mide 90°, por lo que todos los ángulos interiores de P´´  XP´´ P son rectos. En consecuencia, la figura es un rectángulo. 

-Proyección de un segmento sobre una recta: proyectar un segmento sobre una recta dependerá de la posición del segmento con respecto a la recta.
  
1) Si el segmento dado AB no es paralelo la recta L, la proyección ortogonal es segmento PQ que se obtiene trazando líneas perpendiculares a L desde los puntos extremos. La magnitud de la proyección siempre es menor que la del segmento dado.

                                                     

2) Si el segmento PQ y la recta L son paralelos, la proyección será: AB = PQ, que se obtiene de forma análoga.

                                                      

3) Si el segmento AB tiene un punto común con la recta L, la proyección se obtiene de modo similar.

                                                

4) Si el segmento AB corta a la recta L, la proyección se obtiene de forma análoga.

                                          

Ejemplo : Trazar la proyección de AB sobre m y n.

Procedimiento:

 Se trazan por A y B rectas perpendiculares a m para determinar el segmento PQ.

Se trazan por A y B rectas perpendiculares a n para hallar el segmento XY, y obtener la otra proyección buscada.

-Proyección de una figura sobre una recta: La proyección de las figuras planas, es decir, que tienen dos dimensiones: largo, ancho, origina proyecciones en una sola dimensión. Las proyecciones ortogonales de cuerpos, es decir, que tiene tres dimensiones: largo, ancho y alto, son figuras planas; tal como pasa con la sombra de un cuerpo cuando es iluminado por el Sol.